ExpEYES

Distance travelled by a freely falling body is given by the equation $ S = \frac{1}{2}gt^2 => g=\frac{2S}{t^2}$. A mild steel ball is attached to an electromagnet fixed at a height. A contact sensor is kept below. The ball is releasd under program control and the time to reach the contact sensor is measured. The experimental setup is shown below.

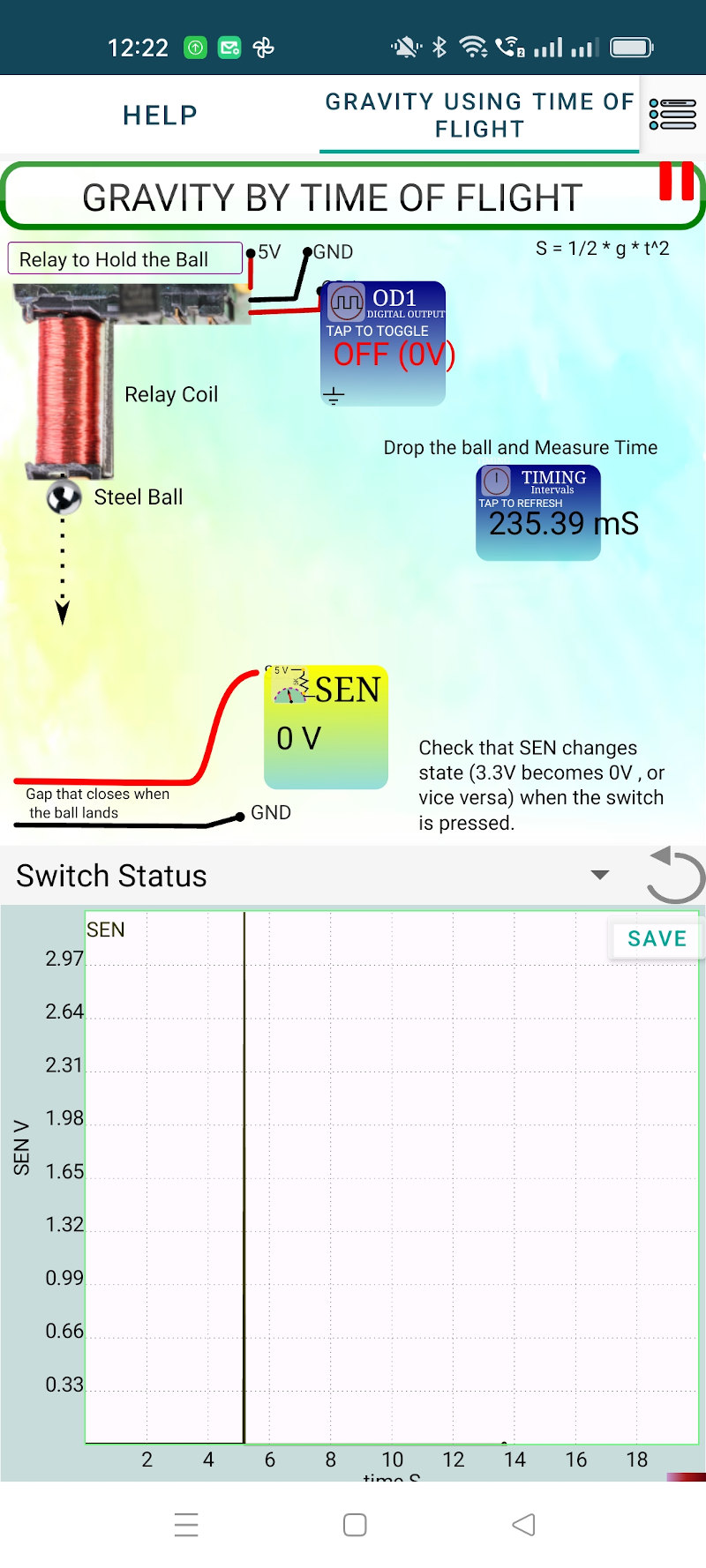
The distance from the lowermost point to the contact sensor is 27 cm. Using the equation $ g = \frac{2S}{t^2} = \frac{54}{0.2354^2} = 974.5 . The value of ‘g’ is very close to the actual value but there are several sources of error.

• We assume that the ball is released at the moment the voltage applied to the electromagnet is removed, but that is not true. It takes several milliseconds, due to the inductance of the coil. One can reduce the error by making the attraction just enough to hold the ball. This can be done by creating a gap between the electromagnet and the ball by placing a layer of cellotape between them.

Python program to perform this experiment.

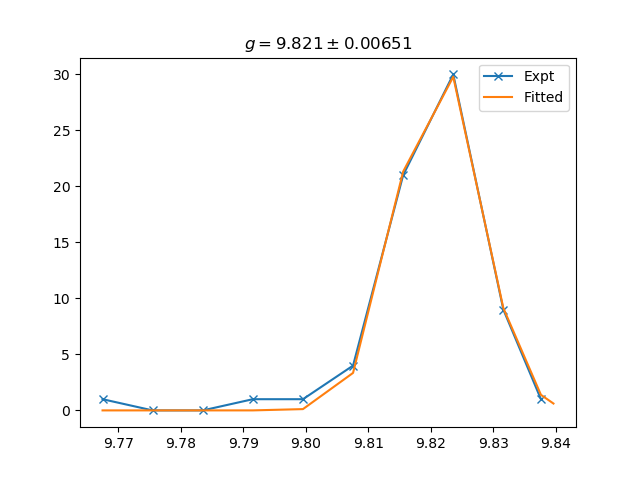
The program given above saves the ‘time of flight’ data to a text file named tof.csv. Perform the experiment a large number of time (around 100 times). To estimate the random error we need to make a histogram of the data and fit it with a Gaussian function. The Python program given below can be used for that.

• Program tof-analyse.py plots the histogram and fits it.